This tutorial offers advice on how to solve trigonometric problems and provides several problems worked through in detail.
It assumes you are familiar with the trigonometric functions sine, cosine, tangent, secant, cosecant, and cotangent. A basic tutorial can be found here. A more advanced tutorial can be found here.

If an explanation / walkthrough is not clear, please let me know in a comment and I will try to improve the answer.
Identify what it is that is not clear – just saying “I didn’t understand it” isn’t very helpful.

If you have a problem you would like to see solved, leave a comment. Note: (1) I don’t do homework, (2) I don’t promise I will solve it, (3) I don’t promise to solve it quickly.

Don’t Panic

Don’t panic or freak out. No one is trying to trick you or trip you up (although, often times, word problems are poorly worded)
Read and understand the problem.
Trigonometric problems are always about right angle triangles. So the trick is to try and break the problem down into right angle triangles.
Trigonometry is about the ratios of the lengths of two sides. If we know the length of two sides of a right angle triangle we can calculate the ratio between those two sides. Those ratios are given special names: sine, cosine, tangent, cosecant, secant, cotangent. Because of the properties of right angle triangles, if we know one of the angles then we also know the ratios of all the sides.
Look for what ratios or partial ratios you can find. Then work from there.
Similar triangles are triangles that have the same shape that have the same angles inside. Often times, we don’t solve the problem directly but look for a similar triangle. The triangle may be bigger or smaller, but it has the same shape as the triangle we are studying.

Basic Use of Trigonometric Definitions

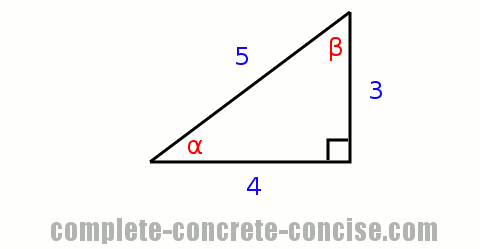
Consider the following right angle triangle having sides of length 3, 4, and 5 units and two angles called alpha and beta. What is sinα, cosα, tanα, sinβ, cosβ, tanβ and the angles α and β?

This problem is about understanding the definition of the trigonometric functions sine, cosine, and tangent.
The triangle is displayed in a familiar way and we can easily calculate the trigonometric relations for α (remember sinα is shorthand for “given a right angle triangle containing an angle α, what is the ratio of the side opposite the angle to the hypotenuse“):
We know that sinα = opposite ÷ hypotenuse, which is 3 / 5 which is 0.6.
We know that cosβ = adjacent ÷ hypotenuse, which is 4 / 5 which is 0.8.
We know that tanα = opposite ÷ adjacent, which is 3 / 4 which is 0.75.
Calculating the trigonometric relations for β is no different, although, we need to correctly identify the opposite and adjacent sides:
We know that sinβ = opposite ÷ hypotenuse, which is 4 / 5 which is 0.8.
We know that cosβ = adjacent ÷ hypotenuse, which is 3 / 5 which is 0.6.
We know that tanβ = opposite ÷ adjacent, which is 4 / 3 which is 1.333...
We don’t know what the angles α and β are, but we can find out. We know that sinα = 0.6 and sinβ = 0.8. All we need to do is find out what angles α and β have a sine corresponding to 0.6 and 0.8, respectively.
Using the inverse sin function (sin^-1) on a calculator, we see that α must be 36.87° for sinα to be 0.6 and β must be 53.13° for sinβ to be 0.8.

Before calculator use was wide spread, you would look up the value in a sine table. You can see a sine table with a resolution of 1 degree over here.

Basic Use and Application of Trigonometric Definitions and Properties of a Right Angle Triangle

Given a triangle having sides of length 1, 2, and 3 units, is this a right angle triangle?

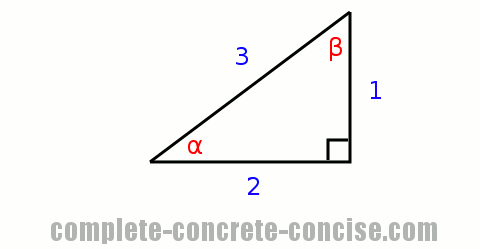
The simplest way is to see if the Pythagorean Theorem true – if this is a right angle triangle, we know that: A² + B² = C²
1² + 2² = 3²
1 + 4 = 9 – the left hand side and right hand side are not the same, so the triangle is not a right angle triangle
Using trigonometric functions, we can determine the angles α and β and then check that all the angles sum up to 180°: α + β + 90° = 180°
sinα = opposite ÷ hypotenuse = 1 / 3 = 0.333…
sinβ = opposite ÷ hypotenuse = 2 / 3 = 0.666…
Using the inverse sin function (sin^-1) on a calculator, we determine that α is 19.47° and β is 41.81°.
Consequently, the sum of the angles is:
19.47° + 41.81° + 90° = 180°
151.28° = 180° – the left hand side and right hand side are not the same, so the triangle is not a right angle triangle

The only thing that might seem strange in this example are expressions of the form:
4 = 9
These types of expressions are perfectly normal and valid in mathematics. This is because the symbol = does not have the same meaning we are usually used to: in mathematics, = means is the same as.
Written in English, the expression 4 = 9 would be “The value of 4 is the same as the value of 9“. This statement is false. Don’t get confused and think you have just proven that 4 is the same as 9 because it isn’t.
In this example, we are saying:

The angles in a triangle sum up to 180°
Since this is supposed to be a right angle triangle, we know one of the angles is 90°
Since this is supposed to be a right angle triangle, we can look up the angles α and β once we know the ratios of the sides
If the sum of all the angles is 180° then we know this is a right angle triangle
If the sum of all the angles is not 180° then we know this is not a right angle triangle.

Calculating the Height of a Tree

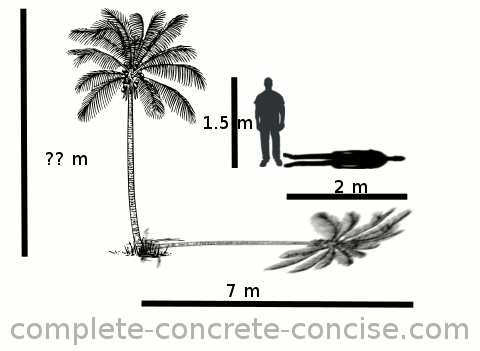
Potiphar’s out walking his cat. He notices that he casts a shadow 2 m long. He also notices that a tree in the garden casts a shadow 7 m long. If Potiphar is 1.5 m tall how tall is the tree? What is the angle of elevation of the sun?

This is a basic trigonometric problem involving similar triangles. Potiphar and his shadow form a right angle triangle. The tree and its shadow form another right angle triangle. The rays of the sun (which are invisible) form the hypotenuse of these right angle triangles.

We know that similar triangles have the same shape and the same angles. We know that the angle or slope of the hypotenuse is the same for both the tree-triangle and the Potiphar-triangle (because rays of sunlight are parallel to each other). Since both triangles are similar, we also know that the ratios of their sides must be the same.
We know the lengths of the sides of the Potiphar-triangle and can use them to calculate a ratio:
A / B = 1.5 / 2 = 0.75
Of the tree-triangle, we know the length of one of the sides but not of the other. However, we know that the ratio of the unknown length to the known length (i.e. shadow) must be the same as for the Potiphar-triangle:
a / b = A / B = 0.75
Plugging in the values we know (and removing the A / B for clarity):
a / 7 = 0.75
Rearranging we get:
a = 0.75 × 7 = 5.25
The tree is 5.25 m tall.
To calculate the elevation of the sun, we know the ratio of height to length. In trigonometric terms, this is the definition of tangent.
tanα = opposite ÷ adjacent = A / B = a / b = 0.75
Looking up (or using the inverse key on the calculator) we see that for tanα to equal 0.75, α must be 36.87°.

Before calculator use was wide spread, you would look up the value in a tangent table. You can see a tangent table with a resolution of 1 degree over here.

Calculating the Height of a Pyramid and Elevation of the Sun

Thales of Miletus measures the length of the shadow cast by the great pyramid and discovers that it is 17 m to the base of the pyramid. Using his 2 m measuring stick he notices that it casts a shadow of 1.8 m. If the great pyramid measures 230 m on a side, how high is the great pyramid? What is the angle of elevation of the sun?

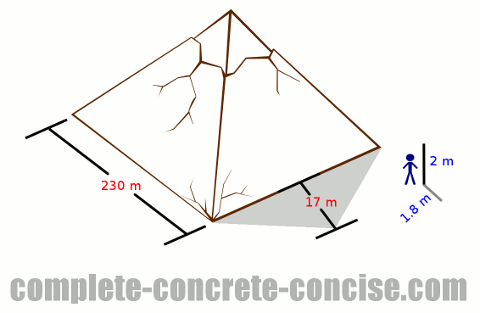
This is another basic trigonometric problem involving similar triangles, but this time a little trickier to solve. We know the dimensions of the height and length of the measuring-stick-triangle, but we don’t know the height or length of the pyramid-triangle. We know the length of the shadow to the base of the pyramid, but we need to know the length of the shadow to the center of the pyramid (from which the height is measured).

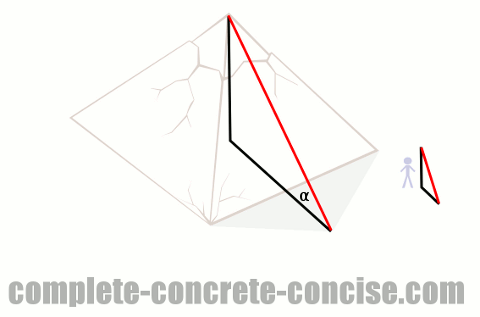
We know the length of a side of the pyramid (this 230 m), we can use this to determine what the length of the shadow to the center of the pyramid should be. The peak of the pyramid is in the center, so it is 115 m from the base of the pyramid. This gives us a corrected shadow length of 17 m to the base + 115 m from the base to the center which is 132 m.
We now know the length of one of the sides of the pyramid-triangle. Since the pyramid-triangle is similar to the measuring-stick-triangle, and we know that similar triangles have the same ratios for their sides, we can calculate the height of the pyramid in the same way as the previous example:

In the previous example (Calculating the HEight of a Tree), I wrote the equation as:
a / b = A / B = ratio
Equations in mathematics can be written in many different ways. In this example, I don’t bother to write the ratio and instead write it as:
a / b = A / B

Substituting the known values we get:
2 / 1.8 = height / 132
Rearranging we get:
(2 × 132) / 1.8 = height
Simplifying everything we get:
height = 146.7 m
To calculate the elevation of the sun, we know the ratio of height to length. In trigonometric terms, this is the definition of tangent.
tanα = opposite ÷ adjacent = 2 / 1.8 = 1.111…
Looking up (or using the inverse key on the calculator) we see that for tanα to equal 1.111…, α must be 48°.

Calculating the Length of a Shadow

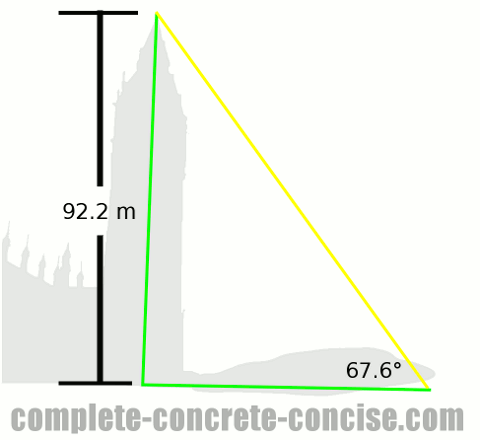
The Peace Tower in Ottawa, Canada is 92.2 m tall. On July 1st, 2012, at noon, the sun’s angle of elevation was 67.6°. How long was the shadow cast by the Peace Tower?

We know the height of the tower and we know the angle of the sun (relative to the ground).
Unlike the previous two problems, we only have one right angle triangle – the tower-shadow-triangle. We know if we have two similar triangles, the ratios of their sides must be the same.
We know the angle the sun makes with the ground, so we know one of the angles of the triangle (actually, we know two of them – the other is 90° – so, if we need to, we can find the third angle because all angles in a triangle must sum up to 180°).
All right angle triangles with the same angles are similar triangles – it doesn’t matter if we don’t know the lengths of the sides because we know the ratios those sides will have.
We know that the following must be true:
length of the opposite side ÷ length of the adjacent side = tan(α)
Plugging in the values we know, we get:
92.2 / x = tan(67.6°)
Evaluating (looking up) tan(67.6°) we get:
9.2. / x = 2.43
Rearranging we get
x = 92.2 / 2.43
Simplifying we get:
x = 37.94
The length of the shadow is 37.94 m (and it is probably safe to round it up to 38 m).

Calculating the Height of a Cliff

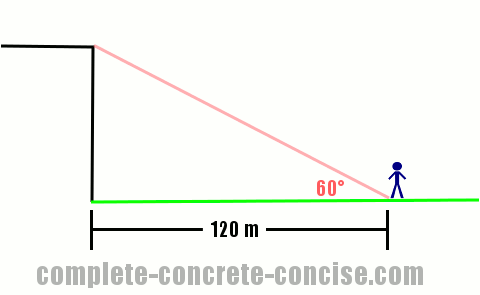
A surveyor measuring the height of the cliff, determines that the angle to the top of the cliff is 60° and the distance to the base of the cliff is 120 m how high is the cliff?

This is similar to calculating the length of the shadow from two examples earlier.
The distance from the cliff, with the height of the cliff and the straight line to the top of the cliff form a right angle triangle.
We know one of the angles. We also know that all right angle triangles with the same angle are similar triangles – this means we also know the ratios the various sides of the triangles have.
As before, we know that:
opposite ÷ adjacent = tan(α)
Plugging in the values we know, we get:
x / 120 = tan(60°)
Evaluating tan(60°) we get:
x / 120 = 1.732
Rearranging we get:
x = 1.732 × 120
Simplifying we get:
x = 207.84
The cliff is 207.84 m high (it is probably ok to round it to 208 m).

How would the problem and solution change if we were given the other angle instead?
In this case, we would have:
120 / x = tan(30°)
When solved it would give us the same answer.
The relationship remains the same, the only things that change are which side we call opposite and adjacent.

Calculating the Height of a Lighthouse

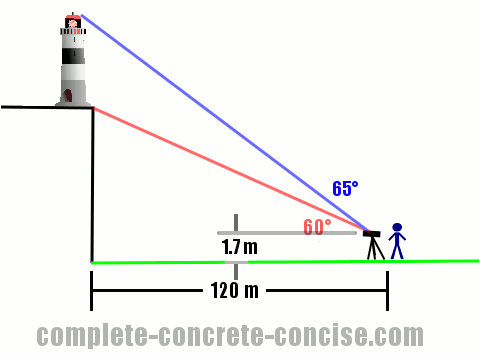
A surveyor measuring the height of the cliff, determines that the angle to the top of the cliff is 60° – this angle was measured at a height of 1.7 m (i.e. the surveying equipment is on a tripod and stands 1.7 m above the ground). The angle measured to the top of the lighthouse is 65°. The distance to the cliff is 120 m. How tall is the lighthouse? How high is the cliff?

In this case, we are given two triangles, but they are not similar. One triangle is the cliff-triangle, the other is the cliff-lighthouse-triangle.
If we find the height of both triangles, we can subtract the height of the cliff from the height of the cliff + lighthouse and get the height of the lighthouse.

Cliff Height

This is basic trigonometric ratios:
cliff height ÷ distance to cliff = tan(60°)
Plugging in the known values:
x / 120 = tan(60°)
Solving:
x = 207.84
We’re not finished with the height of the cliff, the angle to the top of the cliff was measured from a height of 1.7 m, this means we need to add 1.7 m to the height of the cliff:
height = 207.84 + 1.7 = 209.54 m

If we measured from the base of the tripod, what would the angle be to the top of the cliff?

In this case, we know the length of two sides of the triangle: 120 m and 209.54 m.
We can calculate the ratio of these two sides:
ratio = 209.54 / 120 = 1.74616...
We know from trigonometric definitions that tan(α) = opposite ÷ adjacent, so all we need to find is what α gives us the necessary ratio. Using tan^-1 on the calculator we see that:
tan^-1(1.74616...) = 60.2°

Height of the Cliff + Lighthouse

This is basic trigonometric ratios:
(cliff height + lighthouse height) ÷ distance to cliff = tan(α)
Plugging in the known values we get:
x / 120 = tan(65°)
Solving:
x = 257.34
We’re not finished with the height of the cliff + lighthouse, the angle to the top of the cliff + lighthouse was measured from a height of 1.7 m, this means we need to add 1.7 m to the height of the cliff + lighthouse:
x = 257.34 + 1.7 = 259.04 m

Height of the Lighthouse

It is a simple matter of subtracting the height of the cliff from the height of the cliff + lighthouse:
lighthouse height = (lighthouse height + cliff height) - cliff height
Plugging in the known values we get:
x = 259.04 - 209.54
Solving we get:
x = 49.5 m

In this example, it was not necessary to correct the height of the cliff and cliff + lighthouse by adding 1.7 m to each because each was offset (measured) from the same point – but it is still good practice to find the true heights (dimensions) even if only the relative ones are good enough.

Calculating the Length of a Field #1

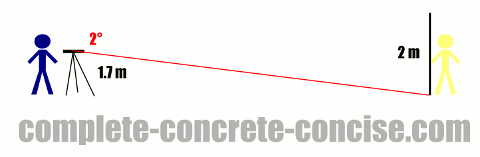
Two surveyors measure the length of the field. One surveyor stands at one end of the field with the measuring equipment, the other surveyor stands at the other end of the field with a measuring stick 2 m high. The surveyor measures an angle of 2° to the base of the measuring stick. The surveying equipment is at a height of 1.7 m. How long is the field?

This is basic trigonometric ratios. The straight line (of sight) to the measuring stick is perpendicular to the measuring stick, therefore, it forms one side of a right angle triangle. The measuring stick (or part of it) forms another side. Finally, the line of sight to the base of the measuring stick forms the remaining side (which is also the hypotenuse):

We know the height where the straight line of sight intersects the measuring stick must be 1.7 m. We also know the angle to the base of the measuring stick is 2°.
We don’t know the length of the side adjacent to the measured angle, we do know the length of the side opposite the measured angle, and we know the angle. Two trigonometric ratios use the opposite and adjacent sides: tangent and cotangent. Since tangent is the more commonly used ratio (and appears on many calculators) we will use the definition of tangent:
tan(α) = opposite ÷ adjacent
Plugging in the known values, we get:
tan(2°) = 1.7 / x
Solving, we get:
x = 48.68
The length of the field is 48.68 m (it is probably safe to round up to 48.7 m)

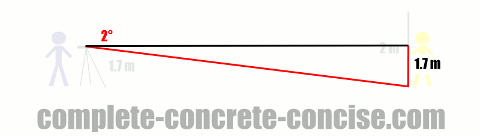
Calculating the Length of a Field #2

Two surveyors measure the length of the field. One surveyor stands at one end of the field with the measuring equipment, the other surveyor stands at the other end of the field with a measuring stick 2 m high. The surveyor forgot to measure the height of the equipment, but, fortunately, took two readings. The surveyor measures an angle of 2° to the base of the measuring stick and 1° to the top of the measuring stick.. How long is the field?

We know the straight line of sight to the measuring stick must be perpendicular to the measuring stick – this forms one side of a right angle triangle (as in the previous example). In fact, it forms the side of two right angle triangles – since two different angles were measured. Unlike the previous example, we don’t know the length of the other side, but we do know the length of the measuring stick – it is 2 m. We know that the sum of the two opposite sides must be 2 m. We also know the angles for both right angle triangles, so we know the ratios the sides have:

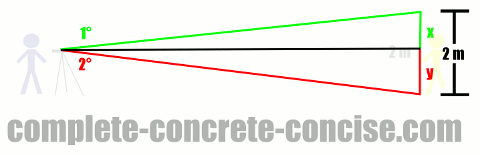
From trigonometric definitions we know that tan(α) = opposite / adjacent
We also know the adjacent side is the same length for both triangles.
Finally, we know that opposite_top + opposite_bottom = 2 m.

Top Triangle

Solving for the top triangle we get:
tan(1°) = opposite_top / adjacent
Calculating what we can, we get:
0.017455 = opposite_top / adjacent

Bottom Triangle

Solving for the bottom triangle we get:
tan(2°) = opposite_bottom / adjacent
Calculating what we can, we get:
0.034921 = opposite_top / adjacent

Combining the Equations

Fundamental to basic algebra is the ability to manipulate an equation any way we like – as long as we do the same thing on both sides.
For example, consider 4 = 4:
We can add 8 to both sides and the relationship remains the same: 4 + 8 = 4 + 8.
However, it is also perfectly valid to do: 4 + 8 = 4 + 1 + 2 + 5 (this is one of those non-intuitive mathematical tricks – but it is very useful).
We need to employ this algebraic trick of substituting equivalent things into our equations.

Since we know that the adjacent sides of both right angle triangles are identical, we can use this to merge the two equations together.
Rearranging the bottom triangle equation so the adjacent is alone, we get:
adjacent = opposite_bottom / 0.034921
We now replace the adjacent side in the top triangle with its equivalent which is opposite_bottom / 0.034921:
0.017455 = opposite_top / (opposite_bottom / 0.034921)
Rearranging we get:
0.017455 × opposite_bottom = 0.034921 × opposite_top

Solving for the opposite_bottom side

Dividing both sides by by 0.017455, we get:
opposite_bottom = 2 × opposite_top

Remembering the 2 m Measuring Stick

At this point, we need to remember that opposite_bottom + opposite_top = 2

It is common in mathematics that you have to remember several things at the same time as you proceed through the steps of solving a problem.

Algebraic Substitution Trick on the Measuring Stick

We can do a similar equivalent substitution in this equation (in this case, we will substitute 2 × opposite_top for opposite_bottom:
2 × opposite_top + opposite_top = 2
Solving we get:
opposite_top = 0.666...

If the top portion of the stick us 0.666… m, then the bottom portion must be 1.333… m

Returning to the original equation:

It does not matter which of the lengths we use (as long as we use them in the right place), the answer will still be the same (any small differences in the answers are due to rounding errors – you can avoid / minimize these by using the full precision provided by your calculator.

Now we can take this value for opposite_top and substitute it our original equation for the top right angle triangle:
tan (1°) = 0.666... / adjacent
Solving we get:
adjacent = 38.19
The distance of the field is 38.19 m (which you can, probably, safely round up to 38.2 m)