The Alternate Interior Angles Theorem states that If two parallel straight lines are intersected by a third straight line (transversal), then the angles inside (between) the parallel lines, on opposite sides of the transversal are congruent (identical).
This is illustrated in the image below:
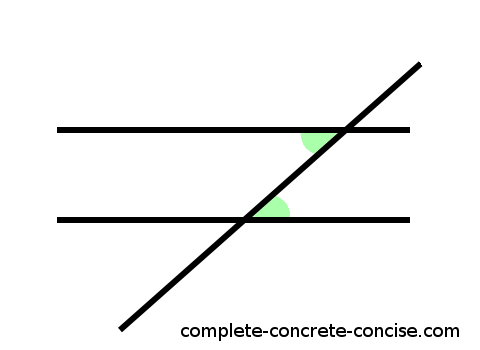
We see two parallel lines and a third line (transversal) intersecting (crossing or cutting through) both of them. The green shaded angles are: (1) inside (between) the two parallel lines, (2) congruent (identical or the same), and (3) on opposite sides of the transversal.
This is true for the other two unshaded interior angles. It is also true for the alternate exterior angles (but not proved here).
Axioms
Proofs are built on two things: (1) postulates, axioms, or hypotheses – these are things that are assumed to be true, but can’t be proved. In general, we try to use the fewest number of axioms we can; (2) other proofs.
This proof depends on two axioms: (1) if you pick any two distinct points on a straight line, the angle between those two points will be 180°; (2) if you take any two intersecting straight lines and shift one of the lines so it it is in a different position, but still parallel to its original position, the angle between the two intersecting lines stays the same.
Proof
1) Consider two intersecting lines:
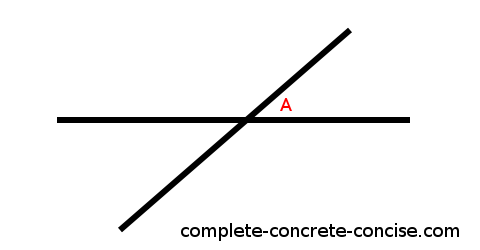
At the point of intersection, there is an angle (which I call A).
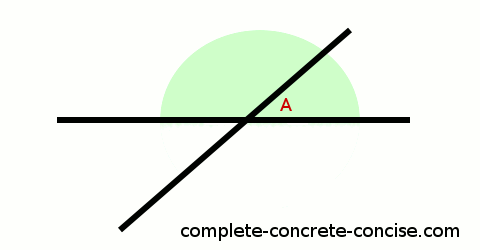
2) If the line is straight, the angle between any two points on that line must be 180° (axiom #1 from above):
3) If one angle is A degrees, then obviously the other angle must be 180° – A:
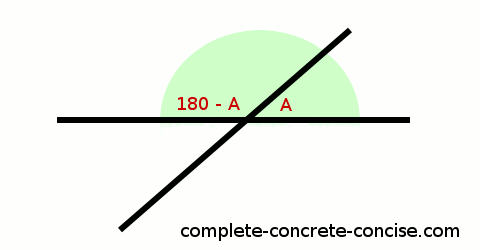
4) This is true for both straight lines:
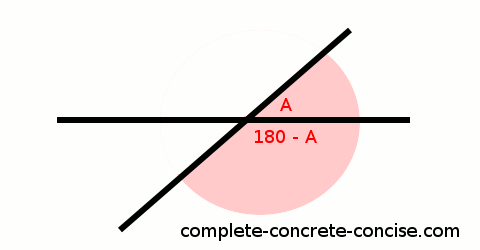
5) This means the remaining angle must be 180° – (180° – A) = A degrees:
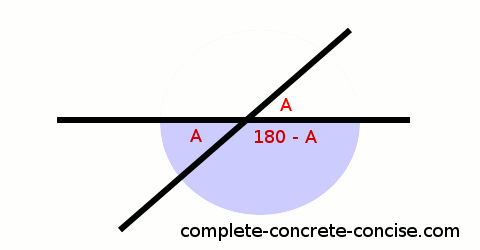
This proves that angles on alternate sides of the transversal (at the point of intersection) are congruent (identical).
6) If we draw a line parallel to one of the lines (it doesn’t matter which) and it intersects the other line (that line is now called a transversal), we know that the angles of intersection must be the same (axiom #2 from above).
If the angles of intersection are the same for both lines, then the alternate interior angles must be the same:
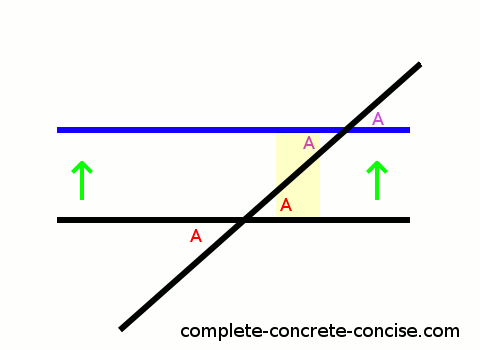
The proof is exactly the same for alternate exterior angles except we focus on the exterior instead of the interior angles (which is illustrated in the image above).