Proving that the angles inside a triangle – any triangle – sum up to 180° is very simple, but leaves most people unsatisfied (or unconvinced) because it depends on the properties of something called Alternate Interior Angles.
I’ll give the proof first and then explain Alternate Interior Angles
A demonstration of the angles of a triangle summing up to 180° can be found here.
Proof
Given any triangle, how can you prove that the angles inside a triangle sum up to 180°?
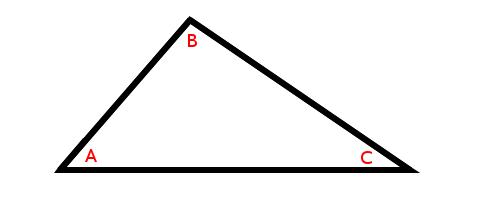
1) Draw a line parallel to one of the sides of the triangle that passes through the corner opposite to that side:
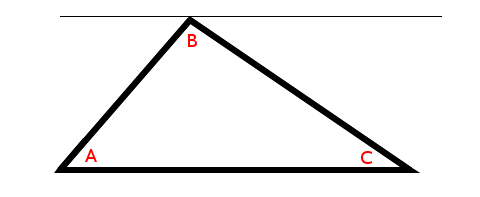
It is easiest to draw the triangle with one edge parallel to the horizontal axis, but you don’t have to because this proof works regardless of the orientation of the triangle. Rotating a triangle does not change its properties.
2) This creates two new angles. We’ll call them D and E:
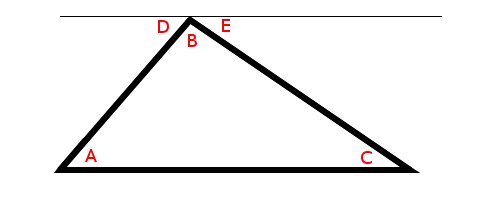
3) We know by Alternate Interior Angles that angle D must be the same as angle A and angle E must be the same as angle C.
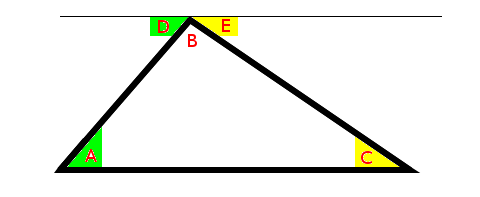
4) Replace the new angles found in step 2) with A and C:
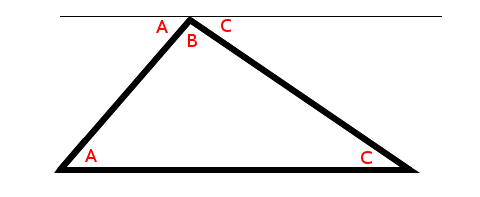
5) We see that angle A + angle B + angle C add up to give us a straight line or 180°:
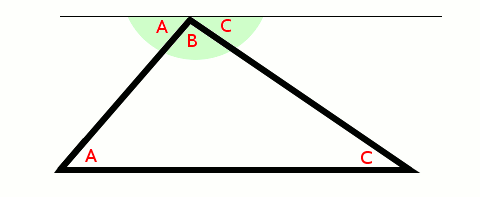
This proof depends on something called Alternate Interior Angles – which makes the proof trivial, but unsatisfying for most people because it is not one of those “facts” we carry around with us.
In fact, pulling out Alternate Interior Angles makes it look like a lot of mathematics is just made up on the spot.
Alternate Interior Angles isn’t pulled out of thin air and it is a fundamental part of geometry.
Alternate Interior Angles
For a proof of Alternate Interior Angles, see this page.
When two lines intersect (cross each other), you get four angles: A, B, C, and D:

It happens that angles A and C are identical and angles B and D are identical.

If we move one of the lines so it remains parallel to its original position (in math-speak, this is called translation), what happens to the angles? Nothing. The angles remain the same. It doesn’t matter where the two lines intersect (cross). Only the angle of intersection matters.
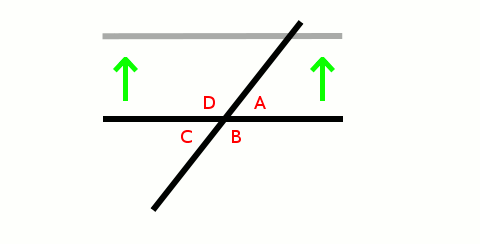
We don’t have to move the line, we can just draw a line parallel to it – we can draw as many parallel lines as we like (but that is likely to confuse things). Each intersection (crossing) has the same angles:

We saw earlier, that A and C are the same angle (as well, as B and D):
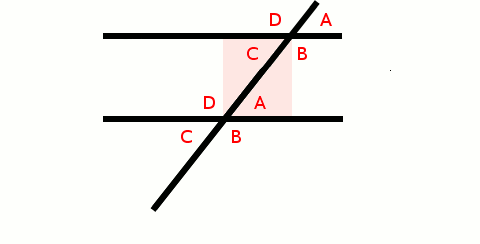
We call the angles between the parallel lines interior angles because they are inside (in between) the parallel lines.
We notice that the angles on opposite sides of the transversal (math-speak for the line that intersects (crosses) the parallel lines) are the same. We say the angles on alternate sides of the line are identical.
Put his all together and you get Alternate Interior Angle
Knowing all this, when we take another look at the proof that all the angles in a triangle sum to 180° we see the following:

1) the base of the triangle forms one of the parallel lines and we draw the second.
2) each of the sides of the triangle acts like a transversal intersecting the parallel lines.
Because angles on alternate sides of the transversal are identical, we are able to sum all three angles and show that they sum up to 180°