A tutorial on the Law of Sines can be found here.
Assumes an understanding of the trigonometric function sine. A basic tutorial can be found here and a tutorial using the Unit Circle can be found here.

The Law of Sines says that “given any triangle (not just a right angle triangle): if you divide the sine of any angle, by the length of the side opposite that angle, the result is the same regardless of which angle you choose”.

The actual value (the result of the calculation) is equal to the diameter of the smallest circle you can draw around the triangle that has all three points of the triangle touching the edge of the circle (a circumscribed circle).
We could state the Law of Sines more formally as: for any triangle, the ratio of the length of a side to the sine of the angle opposite that side is the same for all three sides and is equal to the diameter of the circle which circumscribes the triangle.

To prove the Law of Sines, we need to consider 3 cases:

acute triangles (triangles where all the angles are less than 90°)
obtuse triangles (triangles which have an angle greater than 90°)
right angle triangles (which have a 90° angle)

Acute Triangles

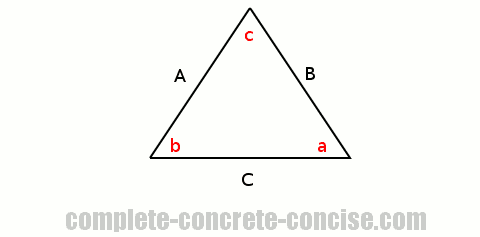
With an acute triangle, we draw a line perpendicular from one corner (vertex) to the side opposite the corner:

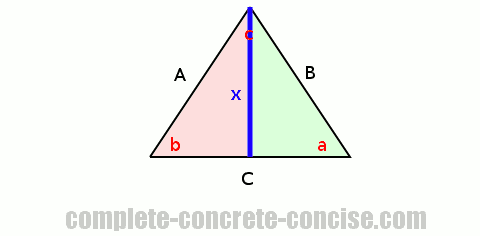
This splits the triangle into two right angle triangles because the perpendicular line forms two 90° angles (one in each new triangle).
Considering the triangle on the left (the pink one), and using the fundamental definition of sine we write:

         x
sin(b) = —
         A

Considering the triangle on the right (the green one), and using the fundamental definition of sine we write:

         x
sin(a) = —
         B

Since x is the unknown term, we rearrange the expressions in terms of x:

x = Asin(b)

and

x = Bsin(a)

We also write the following true (and seemingly silly) expression:

x = x

We can replace each x with something equivalent to x:

x = x  →  Asin(b) = x  →  Asin(b) = Bsin(a)

We can rearrange these by cross multiplying to get:

  A        B
—————— = ——————
sin(a)   sin(b)

This looks a lot like the Law of Sines, but it is not complete, we still need to show that the ratio C / sin(c) is the same as those two.
To do that, we again divide the original triangle into two right angle triangles by drawing a perpendicular line from a different corner to the side opposite that corner:

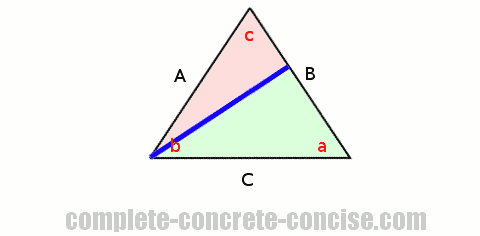
Using exactly the same steps as above, we get:

  A        C
—————— = ——————
sin(a)   sin(c)

If you drew your line from corner a, then you will get B / sin(b) instead of A / sin(a).

We now have two sets of equivalencies, but we know that A / sin(a) must be the same in both equivalencies, therefore we can combine both equivalencies and write:

  A        B        C
—————— = —————— = ——————
sin(a)   sin(b)   sin(c)

Obtuse Triangles

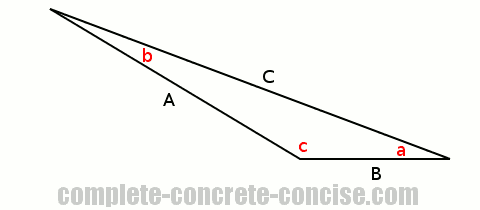
As with the acute triangle, we divide the triangle into two right angle triangles by drawing a perpendicular line from one corner to the side opposite the corner.

Unlike the acute triangle, there is only one such division you can make. In the case of the image above, it is not possible to draw a perpendicular line from either corner a or corner b.

We solve the problem of the two right angle triangles exactly as we did above and get the same result:

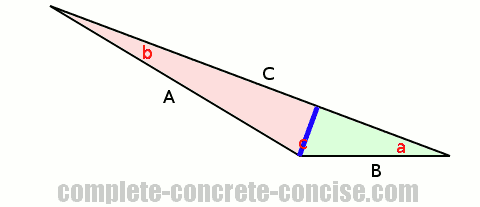
  A        B
—————— = ——————
sin(a)   sin(b)

Because it is not possible to draw another perpendicular line from another corner, we have to use a different technique.
We draw a perpendicular line from one of the other corners to where the opposite side would be if it had continued:

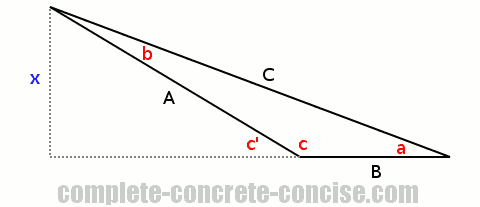
This gives us a right angle triangle for which we can write sine, from its fundamental definition, as:

         x
sin(a) = —
         C

We also have another right angle triangle containing the angle c', a hypotenuse A and an opposite side x, for which we can write sine as:

          x
sin(c') = —
          A

The only problem is that c' is not c. However, sin(c') = sin(c), so we can substitute sin(c) for sin(c').

This looks like one of those “I pulled this out of thin air” statements that we often encounter in mathematics. It’s not really.
Looking at the image, it should be obvious that:

c' + c = 180°

because line segment B and its dashed extension are a straight line – in other words, 180°
Two angles which add up to 180° are called supplementary angles.
If you look at the trigonometric tutorial using the Unit Circle, you will see that angles are measured in a counterclockwise direction from the x-axis. When calculating trigonometric functions for angles greater than 90°, we notice that we can draw an equivalent right angle triangle, but it is flipped (i.e. oriented differently from the “standard” right angle triangle).
There are many supplementary identities, some of which are (for angles less than 90°):

sin(α) =  sin(180° - α)
cos(α) = -cos(180° - α)
tan(α) = -tan(180° - α)

or, if you are using radians:

sin(α) =  sin(π - α)
cos(α) = -cos(π - α)
tan(α) = -tan(π - α)

An identity is simply two mathematical expressions that are the same or equivalent.

Because of the property of supplementary angles we can replace sin(c') with sin(c), thus giving us:

         x
sin(c) = —
         A

As before, we rearrange the expressions in terms of x and get:

x = Asin(c)

and

x = Csin(a)

Just as we did with the acute triangle bove, we can rearrange and equate the two expressions to get:

  A        C
—————— = ——————
sin(a)   sin(c)

Just as for the acute triangle above we have two sets of equivalencies, but we know that A / sin(a) must be the same in both equivalencies, therefore we can combine both equivalencies and write:

  A        B        C
—————— = —————— = ——————
sin(a)   sin(b)   sin(c)

Right Angle Triangles

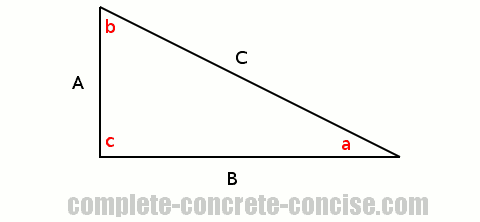
In the previous proofs, we managed to create two right angle triangles for comparison and showed that the ratios of the sine to the length of the opposite side were always the same. It is not possible to do this with a right angle triangle, but we can use the definition of sine to solve it.
From the definition of sine we know that:

         length of the side opposite the angle
sin(α) = —————————————————————————————————————
              length of the hypotenuse

For angle a this is:

         A
sin(a) = —
         C

and for angle b this is:

         B
sin(b) = —
         C

As in the earlier proofs, we can rearrange the expressions (in this case, in terms of C):

      A
C = ——————
    sin(a)

and

      B
C = ——————
    sin(b)

As before, we write the obvious:

C = C

As before, we replace each C with an equivalent expression:

   A        B
—————— = ——————
sin(a)   sin(b)

This is the same as we got before.
We know the definition of sine is opposite / hypotenuse, so we can calculate the sine of the right angle (90°):

           opposite    C
sin(c) =  —————————— = —
          hypotenuse   C

This is perfectly valid, the side opposite the angle is the hypotenuse and the hypotenuse is still the hypotenuse. You can double check that sin(90°) = 1.

Rearranging to express it in terms of C we get:

      C
C = ——————
    sin(c)

Just as for the acute and obtuse triangle, we now have 3 expressions that are equivalent to C (for the previous triangles, it was x – the letter doesn’t matter, only the fact they are equal matters):
Since all the relations are equivalent, we write the down together and get the Law of Sines:

  A        B        C
—————— = —————— = ——————
sin(a)   sin(b)   sin(c)