We learned the Pythagorean Theorem in grade school: The square of the length of the hypotenuse is equal to the sum of the squares of the other two sides. Often written as
A2 + B2= C2.
The Pythagorean Theorem is much more than just a mathematical curiosity, it is a basic and useful mathematical property that shows up as the solution to many mathematical problems or in their proofs (the other two big ones are the right angle triangle and the trigonometric functions – but they are all related).
There are over 300 different proofs for the Pythagorean Theorem, I like this one best. It is simple and only requires some basic knowledge about triangles and some elementary algebra.
1a) Begin with a right angle triangle:
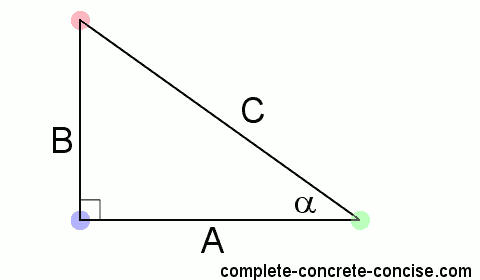
1b) Since this is a right angle triangle, we know one of the angles is 90 degrees (coloured in blue)
1c) For the second angle, we can choose any angle we want. We will call it α (coloured in green)
1d) Because this is a triangle, we know all the angles must add up to 180 degrees. We can use this to find the third angle (coloured in red):
- 90 + α + unknown = 180
- unknown = 180 – 90 – α (grouping the known terms and unknown terms together)
- unknown = 90 – α (simplifying)
We could have called the third angle β (or some other symbol), but calling it 90 – α is a better choice (as we will see).
2) Rotate the triangle so the hypotenuse is horizontal (lying flat). This step isn’t necessary, but makes it easier to see what is happening.
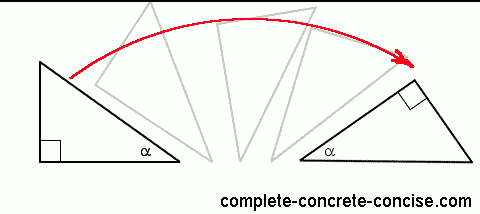
Rotating a triangle does not change its properties.
3a) Draw a perpendicular line from the hypotenuse through the corner opposite it. With the triangle rotated, it is simply a matter of dropping a vertical line from the peak to the hypotenuse.
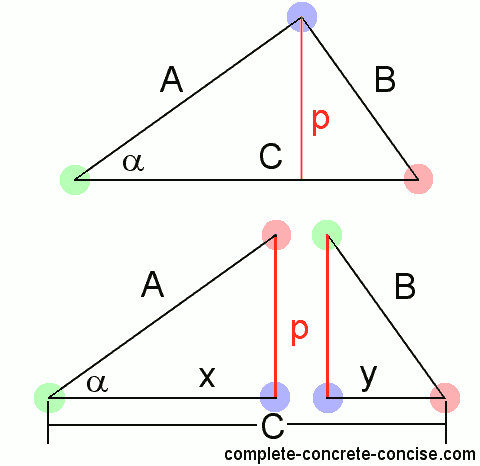
3b) This perpendicular line (which I call p) divides the original triangle into two smaller triangles. Side p becomes one of the sides of both smaller triangles.
3c) The whole of side A went to the triangle on the left hand side.
3d) The whole of side B went to the triangle on the right hand side.
3e) Side C was divided in two. We’ll call the part that went to the left hand side triangle x and the part that went to the right hand side triangle y. Remember that the length of side x plus the length of side y is equal to the length of side C. Mathematically we would write:
x + y = C
The left hand side (LHS) triangle:
4a) We know that one of the angles is 90 degrees. Because line p is perpendicular to the hypotenuse, the angle must be 90 degrees (coloured blue).
4b) When we divided the original triangle, the angle α remained in the LHS triangle, so we know this angle is α (coloured green).
4c) Since the angles in a triangle must add up to 180 degrees, we know that the remaining angle must be 90 – α degrees (coloured red).
4d) Since both the original triangle and the LHS triangle have the same angles, both triangles are similar triangles.
Similar triangles are triangles that have the same angles. The triangles may be different sizes, but the angles are the same.
The right hand side (RHS) triangle:
4e) We know one of the angles is 90 degrees because line p is perpendicular to the hypotenuse (coloured blue).
4f) When we divided the triangle, the angle 90 – α remained in the RHS triangle, so we know this angle is 90 – α degrees (coloured red).
4g) Since the angles in a triangle must add up to 180 degrees, we know that the remaining angle must be α degrees (coloured green).
4h) Since both the original triangle and the RHS triangles have the same angles, they must be similar triangles.
5) In dividing the original triangle, we have created two smaller similar triangles (the original triangle has been rotated and flipped, the LHS triangle has been rotated – I left the text as is):
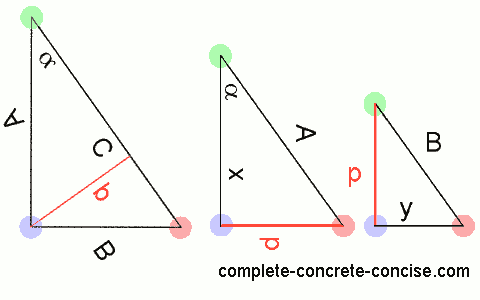
Rotating or flipping triangles does not change their properties.
6) Another property of similar triangles is that the ratio of the lengths of the same sides is the same:
- the ratio of A to B must be the same as
- the ratio of x to p which must be the same as
- the ratio of p to y
Mathematically:
A/B = x/p = p/y
7) We know that the ratio A/C (of the original triangle) = x/A (of the LHS triangle): A/C = x/A.
By cross multiplying, we get: A2 = Cx
8) We know that the ratio B/C (of the original triangle) = y/B (of the RHS triangle): B/C = y/B
By cross multiplying, we get B2 = Cy
Where the magic happens
Fundamental to basic algebra is the ability to manipulate an equation any way we like – as long as we do the same thing on both sides.
For example, consider 4 = 4:
We can add 8 to both sides and the relationship remains the same: 4 + 8 = 4 + 8.
We can do the same with our equation from step (7): A2 = Cx
If we add 33 to both sides we get: A2 + 33 = Cx + 33, but we don’t want to do that because it doesn’t bring us any closer to proving the Pythagorean Theorem
What we want to do, is somehow bring B into the equation (we already have A and C).
We can try A2 + B2 = Cx + B2, but that doesn’t help much (the B2 cancels out).
We need to employ an algebraic trick – we don’t want to add the same thing to both sides of the equation, we want to add equivalent things.
For example, consider 4 = 4. If we add 8 to both sides we would typically do it this way: 4 + 8 = 4 + 8. However, it is also perfectly valid to do: 4 + 8 = 4 + 1 + 2 + 5 (this is one of those non-intuitive mathematical tricks – but it is very useful).
Let us add B2 to the equation from step (7), but this time, we will add the equivalent of B2 to the right hand side. From step (8) we know that B2 = Cy
Using the trick of adding equivalent values to both sides of the equation we get:
A2 + B2 = Cx + Cy
This is very good. We can simplify the right hand side by extracting a common factor:
A2 + B2 = C(x + y)
When we divided the original triangle in step (3a), we divided line C into two parts: x and y. From (3e) we know that x + y = C, so we can replace x + y in the equation above by C:
A2 + B2 = C(C)
When simplified gives us:
A2 + B2 = C2
which is the Pythagorean Theorem.