What is an Identity?

An identity (in mathematics) is something that is true (more precisely: a tautological relationship).

For example, the following is an identity:

1 + 1 = 2

It says that 1 + 1 is exactly the same as 2.

A common (and important) trigonometric identity is:

sin2θ + cos2θ = 1

All this identity says is that what is on the left hand side is identical to what is on the right hand side.

Why Learn / Use Identities?

Identities (in any branch of mathematics) help us to:

• solve
• simplify
• or gain insight into

mathematical problems.

Identities are a lot like synonyms in language. Instead of using the word red to describe the colour of something we could use one of the following: carmine, cherry, copper, crimson, ruby, ruddy, rust, scarlet. In language, synonyms give spice to communication; in mathematics, it is used to look at things in a different way.

For example, if you were solving an trigonometric problem and ended up with the following expression:

cos2θ × tanθ × secθ × cscθ

you might not think you had achieved much. However, by using basic trigonometric identities, you would see (or maybe have to work out) that the entire expression can be reduced to the value of 1.

How Many Trigonometric Identities are There?

There are an infinite number of trigonometric identities. Only a few are useful, the remainder generally ending up as problems and exercises for students to solve.

Reference Image

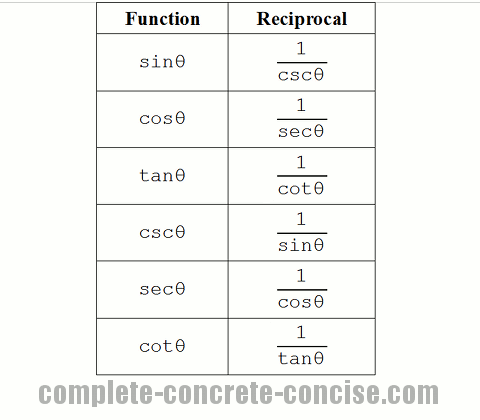
Reciprocal Identities

These identities derive from the fundamental definitions of the trigonometric functions:

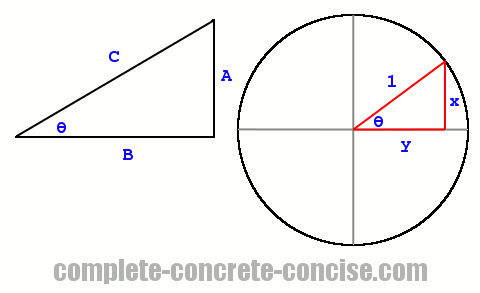
Given a right angle triangle, we know that:

sinθ = A / C

We also know that:

cscθ = C / A

It should be obvious that sinθ = 1 / cscθ because the ratio C / A (cosecant) is the reciprocal of the ratio A / C (sine).

The same reasoning applies to all the reciprocal identities.

Ratio Identities

These identities also derive from the fundamental definitions of trigonometric functions and are very similar to the reciprocal identities, except that they consist of the ratio of two trigonometric functions:

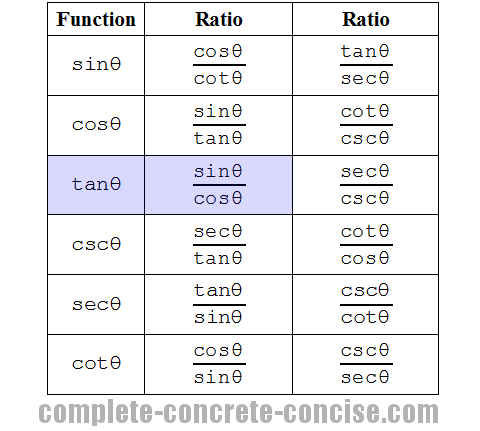
The most important of these is probably tanθ = sinθ / cosθ (highlighted in blue).

We know that

tanθ = A / B     (from a right angle triangle)
tanθ = y / x     (from the unit circle)

We also know that tanθ is the slope of the hypotenuse.

From the unit circle we know that:

sinθ = y
cosθ = x

Using the identities sinθ and cosθ to substitute for y and x, we get the following:

tanθ = y / x = sinθ / cosθ

A similar derivation can be done using the definitions from a right angle triangle:

sinθ = A / C
cosθ = B / C

In order to be able to substitute our identities, we need to multiply both the numerator and denominator by 1 / C

       A   (1 / C)     (A / C)     sinθ
tanθ = - × ———————  =  ———————  =  ————
       B   (1 / C)     (B / C)     cosθ

The same sort of reasoning applies to the derivation of the remaining ratio identities.

sinθ
————  =  1
sinθ

Product Identities

While these can be derived from the fundamental trigonometric identities, it is often easier to use the ratio identities.

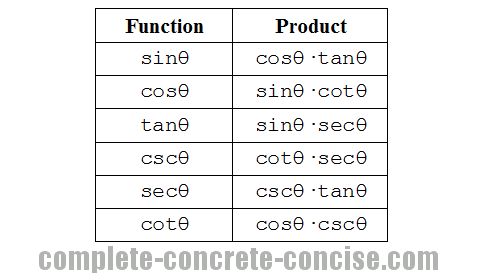
Taking cosθ × tanθ = sinθ, we can derive it as follows:

1) Find an identity for tanθ:

       sinθ
tanθ = ————
       cosθ

2) Substitute this identity for tanθ into the identity cosθ × tanθ = sinθ:

       sinθ
cosθ × ————  =  sinθ
       cosθ

3) Cancel the cosθ terms:

       sinθ
cosθ × ————  =  sinθ
       cosθ

The same sort of reasoning applies to the derivation of the remaining product identities.

sinθ × cscθ = 1

Pythagorean Theorem Identities

Because the trigonometric functions are derived from a right angle triangle and because the trigonometric functions make use of the sides of a right angle triangle, they can be used in the Pythagorean Theorem:

A2 + B2 = C2

sin²θ + cos²θ = 1

This is the most common (or most famous) example of a Pythagorean Theorem identity using trigonometric functions.

It can be arranged in many different ways, the three most common would be:

sin2θ + cos2θ = 1
sin2θ = 1 - cos2θ
cos2θ = 1 - sin2θ

Looking at a right angle triangle, we see that it has 3 sides, normally labelled A, B, and C. With C being the hypotenuse.

Using these sides in the Pythagorean Theorem, we get:

A2 + B2 = C2

To get it to look like sin2θ + cos2θ = 1, we see that we need to get C2 to be equal to 1. This can be done by dividing the entire equation by C2:

A2    B2    C2
—  +  —  =  —
C2    C2    C2

Which gives us:

A2    B2
—  +  —  =  1
C2    C2

This can be rewritten as:

A   A     B   B
— × —  +  — × —  =  1
C   C     C   C

We know that A/C = sinθ and B/C = cosθ, so we can substitute them in the equation giving us:

sinθ × sinθ  +  cosθ × cosθ  =  1

Which, when we collect the terms, gives us the familiar:

sin2θ + cos2θ = 1

1 + cot²θ = csc²θ

Just as we obtained sin2θ + cos2θ = 1 by dividing the terms in the Pythagorean Theorem by C2, we can divide all the terms in the Pythagorean Theorem by A2, which gives us:

A2    B2    C2
—  +  —  =  —
A2    A2    A2

By using similar steps as above, we get the identity:

1 + cot2θ = csc2θ

Three more common arrangements would be:

cot2θ = csc2θ - 1
csc2θ = cot2θ + 1
csc2θ - cot2θ = 1

tan²θ + 1 = sec²θ

Just as we obtained sin2θ + cos2θ = 1 by dividing the terms in the Pythagorean Theorem by C2, we can divide all the terms in the Pythagorean Theorem by B2, which gives us:

A2    B2    C2
—  +  —  =  —
B2    B2    B2

By using similar steps as above, we get the identity:

tan2θ + 1 = sec2θ

Three common arrangements would be:

tan2θ = sec2θ - 1
sec2θ = tan2θ + 1
sec2θ - tan2θ = 1

Trigonometric Identity Problems

All of the following are trigonometric identities. Feel free to verify / prove using the identities described in the tutorial:

  csc2θ
—————————  =  cot2θ
tan2θ + 1

(1 - sin2α)(1 + tan2α) = 1

sec2φ - 1
—————————  =  sin2φ
  sec2φ

sinβ + cosβcotβ = cscβ

1 - sin4γ - 2sin2γcos2γ = cos4γ

It should be obvious that you can create as many identities as you like. It should also be obvious that most (all?) of these are not as useful as the fundamental identities described in this tutorial.

sin2θ + cos2β = 1