A formal definition of the radian is:
One radian is the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle. – Wikipedia
A better (simpler) definition at Math Open Reference is:
One radian is the angle made at the center of a circle by an arc whose length is equal to the radius of the circle.
What they are saying is:
If you have a circle and pick a point on its edge (perimeter / circumference) and travel along that edge a distance equal to the length of the radius (the distance from the center of the circle to its edge), then the angle, at the center of the circle, between those two points is equal to one radian.
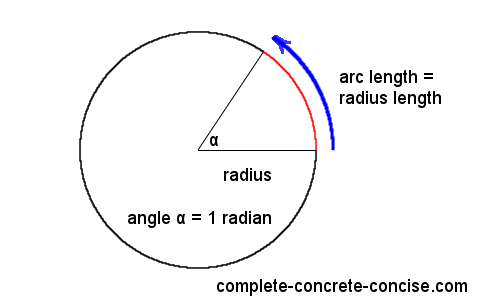
One radian is just shy of 57.3 degrees (57.295779513… degrees – the number is both irrational and transcendental).
Needless to say, radians seem a strange way to measure angles – especially since there aren’t even a whole number of radians in a circle (there are 2π radians in a circle). What’s wrong with using degrees?

How we divide a circle is arbitrary. We use 360 degrees for a circle because that’s how the ancient Egyptians divided their year (the remaining 5 days were set aside as a festival for the gods Osiris, Horus, Set, Isis and Nephthys – one day each). The 360 day cycle of the year became the 360 degrees of a circle.
A circle could just as well be divided into 4 or 8 or 16 parts. It would definitely be easier than dividing a circle into 360 parts. The French divided the circle into 400 parts (100 parts for each quarter circle), following the French Revolution, in their quest to make everything metric (this is the grad or gradian you see on most scientific calculators).
In some ways, radians is a more “natural” division of the circle. A radian is equal to rotating the edge of a circle through a distance equal to the radius, whereas one degree is equal to one-three-hundred-sixtieth of a rotation of the circle. The radian is defined in terms of the circle, whereas degrees are an arbitrary division of the circle.
Another “natural” division could have been to use the diameter of the circle (perhaps we could call them diamens – not a real word, I made it up). In that case, there would be π diamens in a circle.
Dividing a circle into radians has advantages:
If you have a wheel, converting from rotation (angular displacement) to distance (linear displacement) is very easy – multiply the number of radians rotated by the length of the radius to calculate the distance. Converting degrees rotated into distance is much less fun.
For example:
How far does a wheel with a radius of 20 cm travel if it rotates 1 radian? [Remember, in one radian the length of the curve is equal to the length of the radius.]
1 radian x 20 cm = 20 cm (radians, like degrees are dimensionless)
The same problem using degrees is not as easy:
How far does a wheel with a radius of 20 cm travel if it rotates 57.3 degrees?
- the circumference of the circle (the length of the edge) is equal to 2π x length of the radius
- the length of the circumference : 2π x 20 cm = 125.7 cm
- multiply the length of the circumference by the fraction the wheel turned (57.3 / 360 = 0.1597)
- 0.1597 x 125.7 cm = 20 cm (using values from the steps 1, 2, & 3)
- or (57.3 / 360) x 2π x 20 cm = 0.1597 x 6.28318 x 20 cm = 20 cm (all the steps in one line)
Try another example:
How far does a wheel with a radius of 20 cm travel if it rotates 50 radians?
How far does a wheel with a radius of 20 cm travel if it rotates 2864.8 degrees?
The answer is 1000 cm (or 10 m) – much easier to compute using radians.
The advantage of using radians is that it takes the term 2π out of the equation – thus simplifying calculations. There are 2π radians in a circle, consequently, one radian is equal to 1 / 2π of a circle.
We know that ~57.3° equals 1 radian which is equal to 1 / 2π of a circle. If, instead of using degrees, we use its equivalent in radians then we get: (some fraction of a radian) x (1 / 2π) x 2π x (length of radius). The terms 2π cancel out and we are left with (some fraction of a radian) x (length of radius).
In problems dealing with waves (electronics, audio, etc), working with radians instead of degrees makes the computations easier. The factor 2π appears frequently in these calculations and can be eliminated if we deal in radians. This (1) simplifies calculations and (2) reduces error in the calculations – both round off errors and the chance of making errors (consider constantly multiplying or dividing by 2π – or its approximation, 6.28318 – multiplication errors are possible, round off errors a definite possibility). If we need to convert back to degrees, then we can do so at the end.