An article explaining trigonometric functions using the unit circle can be found here

Using the unit circle is the standard way trigonometric functions are defined and understood in mathematics.

I recommend reading and understanding this article first. Later, if you want to understand how trigonometric functions are defined for values greater than 90° or less than 0°, go and read the other article.

Sine is often introduced as follows:

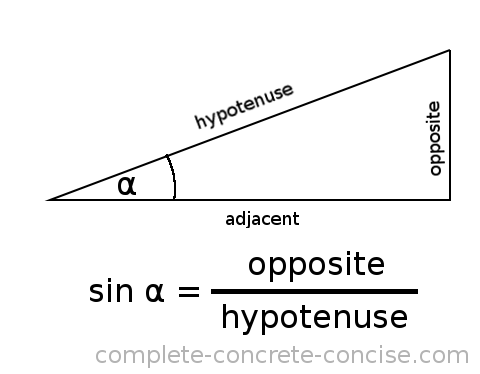
Which is accurate, but causes most people’s eyes to glaze over.

The problem is that from the time humans starting studying triangles until the time humans developed the concept of trigonometric functions (sine, cosine, tangent, secant, cosecant and cotangent) was over 3000 years.

A Little History

The ancients studied triangles. One of the things they did was to compare the lengths of the sides of triangles:

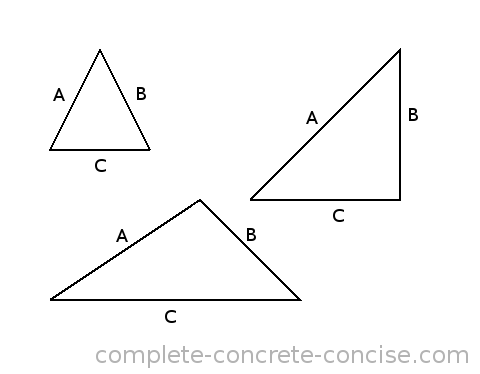
A triangle has three sides so there are 6 different ways to compare sides:

A to B, A to C, B to C, B to A, C to A and C to B

Normally, we would write these as fractions:

A   A   B   B   C   C
-,  -,  -,  -,  -,  -
B   C   C   A   A   B

What they discovered was that if two triangles have the same ratios for their three sides, then the triangles are the same shape – they have the same angles inside even though the size of the triangles may be different.

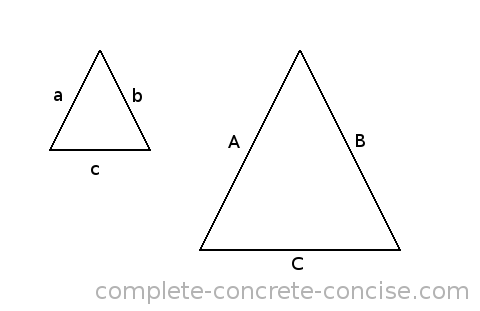
This turned out to be very, very useful because it meant that if you could find a smaller triangle that had the same shape as a larger triangle, then you could study the smaller triangle and find out things about the big triangle. It works the other way around as well, if you have a very small triangle and can find a larger, easier to work with triangle, then you can study the larger triangle and learn things about the smaller triangle. These types of triangles are called similar triangles.

One of the earliest uses of this was shadow reckoning – using shadows to measure things.

Suppose you want to measure the height of a tree, how would you do it?

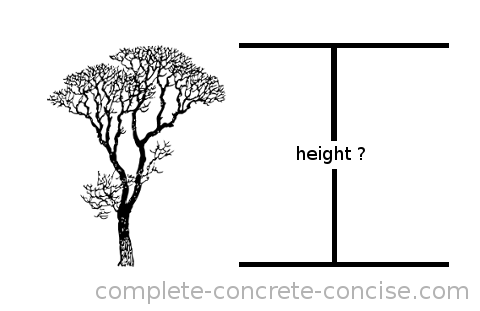
You could climb the tree while carrying a length of rope. You would lower the rope until it reached the ground, mark the length of the rope and then measure the length of the rope (once you climbed down). Unfortunately this is (1) slow, (2) dangerous (there is always the risk of falling), and (3) possibly inaccurate since it is not always possible to climb to the very top of a tree (trees trunks and branches get thinner near the top and they may not be strong enough to support you climbing all the way to the top).

You could cut the tree down and then measure it. But if you want to keep the tree, cutting it down is not an option (it is also pretty slow).

What if you wanted to measure the height of a building or a cliff? Using a rope would work (assuming the rope is long enough), but cutting it down wouldn’t.

However, the ancients noticed that the tree (or building, or cliff) forms one side of a right angle triangle (we’ll assume the tree is growing vertically instead of at an angle), its shadow forms the base of a right angle triangle and the rays of sunlight form the hypotenuse.

If we can make a smaller right angle triangle with the hypotenuse at the same angle as the rays of sunlight, then we have a similar triangle. We can then measure the smaller (and similar) triangle and apply what we know about it to the larger triangle:

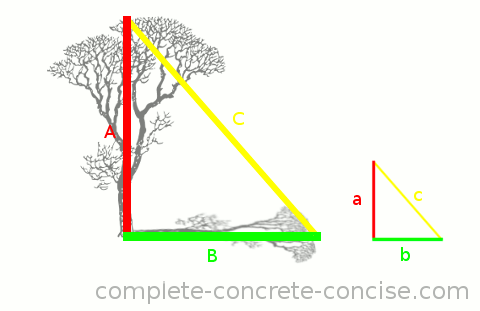
Because the large and small triangle are similar, it means the ratios of the sides are the same. If we have a stick of a known length and place it perpendicular to the ground (this is side a of the small triangle), it will cast a shadow and we can measure the length of that shadow (this is sideb of the small triangle). We can easily measure the length of the shadow cast by the tree (this is side B of the large triangle. Because the two triangles are similar, we know that the ratio a/b must be the same as the ratio A/B.

NOTE: it doesn’t matter if the ratio is calculated as a/b or b/a – as long as it is calculated the same way for both triangles.

If our measuring stick is 2m tall and it casts a shadow 1.25m long, the ratio a/b is 1.6. Because the triangles are similar, we know that the ratio A/B must be 1.6. If the tree casts a shadow that is 15m long we can plug that number into the equation and write A/15 = 1.6. Multiplying both sides by 15 gives us: (A/15)*15 = 1.6*15. Multiplying through we get A = 24, so the height of the tree is 24m.

Definitely try this at home. Calculate the height of your house by measuring the length of its shadow and relating that to the length of a known measure (a yardstick (or meter stick) is good – if you don’t have a yardstick or meter stick, you can always use a 12 inch (30cm) ruler). Or measure the heights of trees in your neighbourhood.

Thales of Miletus used this technique to measure the height of the Great Pyramid (which was already some 2000 years old by the time Thales measured its height):

Thales waited until the shadow was inline with one face of the pyramid and then measured the length of the shadow plus half the length of the base to get the length of side B of the similar triangle. Obviously he had a measuring stick whose shadow he also measured.

Eventually, somebody realized that instead of always measuring the sides of a triangle and computing the ratios you could create a lookup table which had the ratios for right-angle triangles with various angles.

We know triangles are similar if:

the ratios of the 3 sides are the same or
all the angles are the same or
two sides have the same ratio and one angle is the same (as long as it is not between the two sides)

We can tell if two right-angle triangles are similar by simply measuring one angle – as long as it is not the square (90°) angle. Because all the angles in a triangle must add up to 180° we can easily find the 3^rd angle (180° – 90° – measured angle = remaining angle)

Any other lookup table would require we measure at least two sides and calculate their ratio.

The earliest indication we have of someone doing this is Hipparchus of Nicaea who, in the 2^nd century BCE, compiled a table of trigonometric ratios (these were chords and are related to, but not the same as our trigonometric ratios). The mathematics of the Greeks ended up in India and was worked upon by Indian mathematicians, their work was then taken and worked further by the Arabs who (by the 9^th century) had developed the modern notion of the six trigonometric functions we use and had lookup tables for right-angle triangles with different angles. Around the 12^th or 13^th century the work of the Arabs arrived back in Europe and was translated from Arabic into Latin, the term sinus (from which we get sine) was the translation used for the Arabic word jiba – both of which mean fold. Had the scholars not translated the word, we might be using jiba or jib or something similar instead.

You can read more about the history of trigonometric functions here, here, and here. [NOTE: these are external links and were deemed to be working, safe, and on topic at the time of this article. While I double check links from time to time, I make no guarantee about them. I also appreciate being told if the links are not working or no longer valid.]

Sine

When we ask, “What is the sine of 30°?” the answer doesn’t really have much to do with the angle. The angle describes which right-angle triangle we are talking about and which two sides of the triangle we are interested in – but the answer is the ratio of the lengths of those two sides.

A better way to ask the question would be:

“Given a right-angle triangle that has an angle of 30°, what number do we get when we divide the length of the side furthest away from the angle by the length of the hypotenuse?”

Saying sin(30), is a shorter way of expressing that previous (long) sentence:

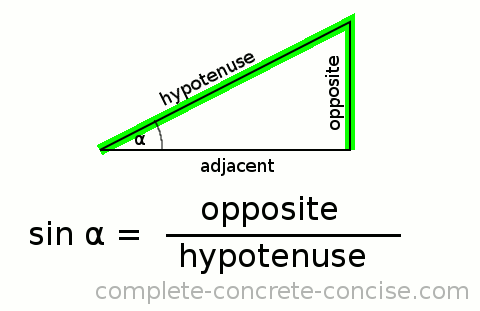
Things to remember:

the value of sine is always between 0 and 1 (more accurately, it is between -1 and 1)
one of the sides is always the hypotenuse (the longest side) and it is always the denominator
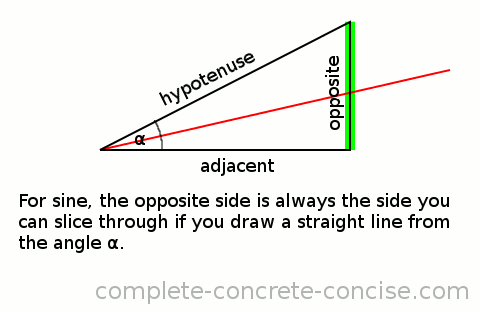
the opposite side can be sliced by a line from the angle in question (Sine and Sliced both begin with the letter S)

Cosine

When we ask, “What is the cosine of 30°?” the answer doesn’t really have much to do with the angle. The angle describes which right-angle triangle we are talking about and which two sides of the triangle we are interested in – and the answer is the ratio of the lengths of those two sides.

A better way to ask the question would be:

“Given a right-angle triangle that has an angle of 30°, what number do we get when we divide the length of the side closest to the angle by the length of the hypotenuse?”

Saying cos(30), is a shorter way of expressing that previous (long) sentence:

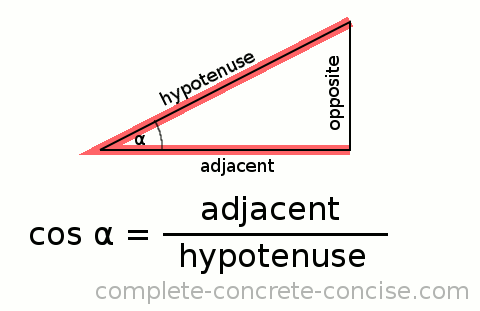
Things to remember:

the value of cosine is always between 0 and 1 (more accurately, it is between -1 and 1)
one of the sides is always the hypotenuse (the longest side) and it is always the denominator
the adjacent side is the one that is connected to the angle (Cosine and Connected both begin with Co)

Tangent

When we ask, “What is the tangent of 30°?” the answer doesn’t really have much to do with the angle. The angle describes which right-angle triangle we are talking about and which two sides of the triangle we are interested in – and the answer is the ratio of the lengths of those two sides.

A better way to ask the question would be:

“Given a right-angle triangle that has an angle of 30°, what number do we get when we divide the length of the side furthest away from the angle by the length of the side closest to the angle?”

Saying tan(30), is a shorter way of expressing that previous (long) sentence:

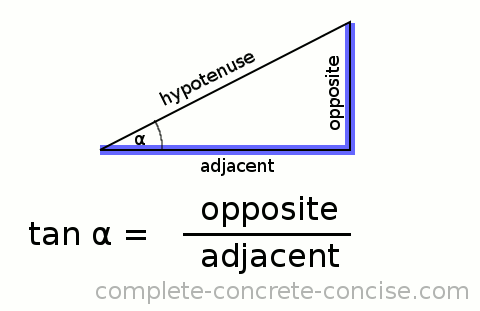
NOTE: the tangent is the same as the slope of the hypotenuse.

This is important to know / remember when learning Calculus and you hear about the tangent line to a point on a curve. In fact, anytime you hear “tangent line” it means the “slope of the line”

Things to remember:

the value of tangent is always between 0 and undefined (sometimes, inaccurately, called infinite ∞ – it is more accurate to say “the slope tends to infinity”). As for sine and cosine, it can be positive or negative.
the hypotenuse is not used in calculating the tangent
the tangent is the same as the slope of the hypotenuse
slope is always rise divided by run (height divided by length)
the run (length) is the side connected to the angle (if you were standing where the angle was, you would be standing on the side)
the rise (height) is the side furthest from the angle (if you were standing where the angle was and looked at the side, you would see it rising up)

Secant, Cosecant, and Cotangent

Secant, cosecant, and cotangent are the other three trigonometric functions and they are the inverse of the first three trigonometric functions.

Cotangent

This one is easy, it is the inverse of tangent. Instead of calculating the slope of the hypotenuse, we calculate the inverse of the slope.

cot α = adjacent / opposite (or run / rise)

Secant

Secant is NOT the inverse of sine. Secant is the inverse of cosine.

We invert both the way we calculate and the way we name the function.

sec α = hypotenuse / adjacent

Cosecant

Cosecant is NOT the inverse of cosine. Cosecant is the inverse of sine.

We invert both the way we calculate and the way we name the function.

Pay Attention to Detail

Oftentimes, the right angle triangle is drawn this way:

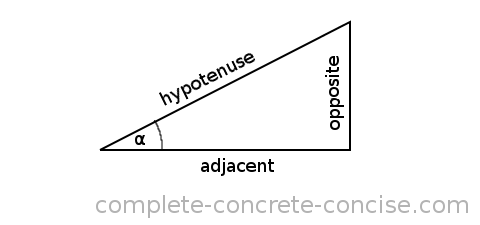
However, the triangle and given angle can be drawn any which way, so it is important to properly identify which sides are which:

The hypotenuse is green.

The adjacent side is blue.

The opposite side is red.

Mnemonic

Nowadays, math seems to focus on teaching “math words” – acronyms or mnemonics that help in remembering the concept. For the trigonometric functions, the following is used: SOH-CAH-TOA (pronounce ‘soh kah toe ah’). It is supposed to help remember the trigonometric function and which sides give which answer.

SOH – Sine = Opposite ÷ Hypotenuse.

CAH – Cosine = Adjacent ÷ Hypotenuse.

TOA – Tangent = Opposite ÷ Adjacent.

To make it easier to remember, the letters are used as the first letters in a whimsical sentence. I created these two because they use homonyms (sound-a-like words) for the trigonometric functions:

Imagine you have just bought something and there is some paperwork to fill out:

Sign Over Here. Co-sign At Home. Take Ownership Anytime.

Imagine you are signing up for a vacation and get some friendly advice at the end. This one does have an extra (unused) word at the end, but it has a homonym for each trigonometric function:

Sign Over Here. Co-sign At Home. Tan Only At night.

This article uses modified tree and pyramid images from The Open Clip Art Library. While the artwork is public domain and does not require attribution, I think it is important and polite to acknowledge sources.