Supplementary and complementary angles are useful concepts to understand in trigonometry.

Supplementary angles are any two angles that sum (add) up to 180° (a straight line).

An easy way to remember this is that Supplementary and Straight line both begin with the letter ‘S’.

Complementary angles are any two angles that sum (add) up to 90° (a corner).

An easy way to remember this is that Complementary and Corner both begin with the letter ‘C’.

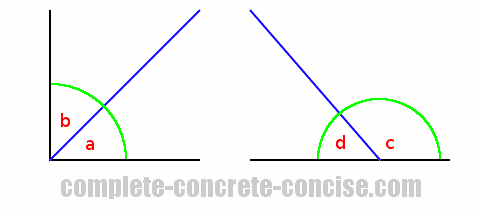
In the above image, we see that angles a and b sum up to 90°, therefore they are complementary angles.

In the above image, we see that angles c and d sum up to 180°, therefore they are supplementary angles.

While the angles were drawn adjacent to one another, they don’t have to be – although, that is the most common way you will encounter them – any two angles that add up to 90° or 180° are complementary or supplementary angles.

Why is this Useful?

This is useful, because it helps in solving trigonometric problems.

For example, consider a construction in which A and B are supposed to be perpendicular. Unfortunately, you can’t measure the angle directly because there is a support beam that comes out from the corner. How can you determine if the walls are perpendicular?

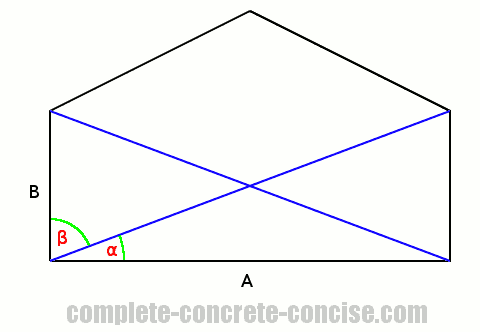
We know that walls (or beams or forces or whatever) are perpendicular if the angle between them is 90°

We can measure angle α and angle β and if they are complimentary, then we know the walls are perpendicular.

This is a contrived example, but, in many proofs, recognizing complementary and supplementary angles is an important part of solving the problem.

For an example of using supplementary angles in proof, see the article Proving the Law of Sines (the section on proving for obtuse triangles)

You can prove alternate interior angles are congruent using complementary angles.

Also see the article Proving Alternate Interior Angles are Congruent for a long winded, but easy to understand proof that does not use complementary angles.

Using complementary angles, the proof can be made like this:

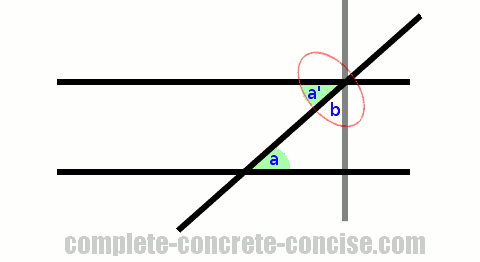
Given two parallel lines and a transversal, draw a line perpendicular to the parallel lines passing through the intersection of the transversal and one of the parallel lines. This creates a right angle triangle.
Acute angles a and b are complementary.
The perpendicular line passing through the intersection of the transversal and one of the parallel lines forms a right angle which is bisected (divided) by the transversal.
Angles a' and b formed by this bisection are complementary, consequently, a' = a