While trigonometry is used to solve problems involving right angle triangles, it can also be applied to triangles that are not right angle triangles.
Assumes you understand basic trigonometric concepts.
A tutorial on understanding sine, cosine and tangent can be found here.
A tutorial on understanding the trigonometric functions and the unit circle can be found here.
What is the Law of Sines
One of the fundamental properties of two triangles that have the same shape (i.e., they have the same angles) is that the ratio of any two sides is identical – regardless of the size of the triangles.
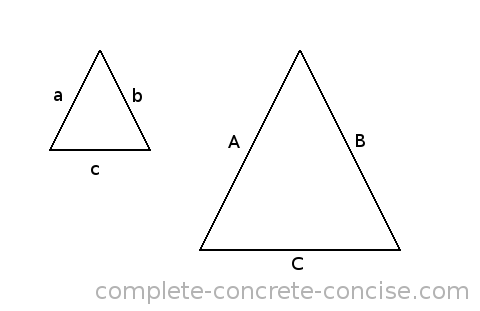
a A a A b B
— = — and — = — and — = —
b B c C c CThis property allows you to study a more conveniently sized triangle to learn things about an inconveniently large or small triangle (for example, a triangle formed by the Earth, moon and sun, or a triangle of forces formed by the interaction of atoms or molecules).
The trigonometric functions were developed for right angle triangles because they made it easier to solve problems.
Surprisingly, the trigonometric function sine can be applied to any type of triangle – provided you know how.
Trigonometry is about ratios and relationships and the Law of Sines is about ratios, specifically, the ratio of a side to the sine of the angle opposite that side is the same for all the sides and angles:

Example
Consider a tree which grows at an angle of 80° relative to the ground. If the measured angle to the top of the tree is 30° and the distance from the measured angle to the base of the tree is 100m, how tall is the tree? How high does the tree stand?
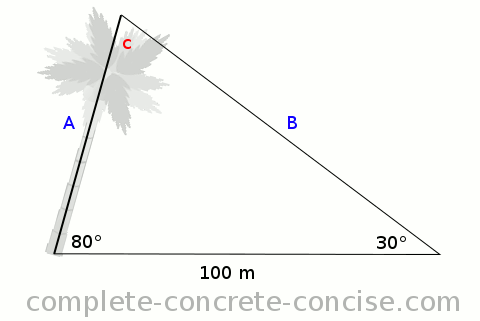
Using the Law of Sines, we know that the following relations are true:
A B C
——————— = ——————— = ———————
sin (a) sin (b) sin (c)Since the height of the tree is A, we are only interested in the following relationship:
A C
——————— = ———————
sin (a) sin (c)We know the angles in a triangle sum to 180°, so we know c = 180° - 80° - 30° = 70°.
Substituting into our Sine Law relation we get:
A 100
———————— = ————————
sin (30) sin (70)Cross multiplying we get:
100 × sin (30)
A = ——————————————
sin (70)Solving, we get a height of 53.2m for the tree.
To solve how high the tree stands, we solve it using both standard trigonometry and the Law of Sines to show they give the same answer:

Using standard trigonometry:
- Drop a perpendicular line from the peak. This is the the height the tree stands. I call it
h. - Use the definition for
sine:sinθ = opposite / hypotenuse - Rearrange the definition of
sine:opposite = hypotenuse × sinθ - Plug in the known values and solve:
opposite = 53.2 × sin(80°) = 52.4m
Using the Law of Sines
Examining the triangle from a Law of Sines point of view, we see:
- The length of the hypotenuse is 53.2m and the angle opposite it is 90° – this gives us one ratio
- While the length of
his unknow, we do know the angle opposite is 80° – this gives us the other ratio
Writing the ratios together we get:
h 53.4
———————— = ————————
sin (80) sin (90)When we solve this through, we get the same answer as using standard trigonometry.