While I call this advanced, it does not mean harder or more complicated, it just means more abstract. Understanding the trigonometric functions (sine, cosine, tangent) using right angle triangles is simply a special case of trigonometric functions using the unit circle.
I strongly recommend first reading and understanding the article Understanding Sine, Cosine, and Tangent first, because it explains the history and reasoning behind the trigonometric functions.
This is the way trigonometric functions are generally understood and defined in mathematics.
Trigonometric functions were originally developed and understood from the study of right angle triangles. The problem with using right angle triangles is that trigonometric functions can only be defined for angles between 0° and 90°, but not for angles ≤ 0° or ≥90° because no such right angle triangles exist.
The Unit Circle
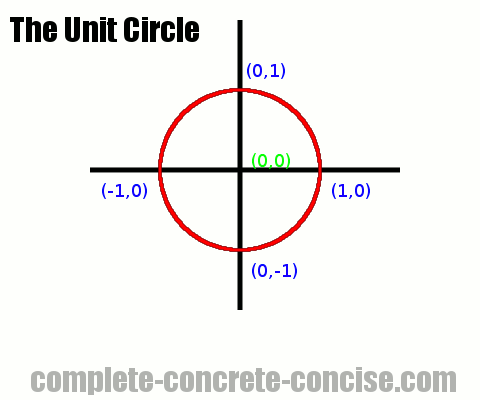
The Unit Circle is a common tool in mathematics. It is a circle with a radius that is one unit long.
How long is a unit? It doesn’t matter. A unit could be 3cm, or 5 inches, or 27 light years. It doesn’t matter how long the radius is, as long as we agree that whatever the length of the radius we will call that length one unit.
Having a unit circle means that we know the diameter is two units long and the length of the circumference (perimeter) is 2π units long.
The unit circle (almost) always has its centre at (0,0). This is certainly true for the trigonometric functions.
Because the unit circle is centred at (0,0) and has a radius of one unit, we know that it intersects (crosses) the X and Y axes at (1,0), (0,1), (-1,0), and (0,-1).
Circling the Triangle
Trigonometry is about triangles. The word trigonometry comes from the Greek trigonometria (trigono = triangle and metria = measure). Going from a triangle to a circle may not seem obvious:
1) Draw a circle
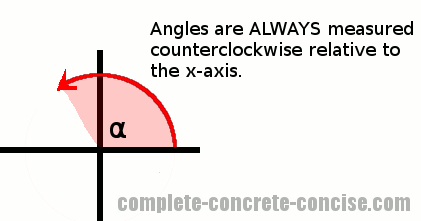
2) Draw a line from the centre of the circle to the perimeter. You can draw the line at any angle you like, but make it greater than 0° and less than 90° (just for now)
NOTE: Angles are ALWAYS measured counterclockwise from the x-axis:
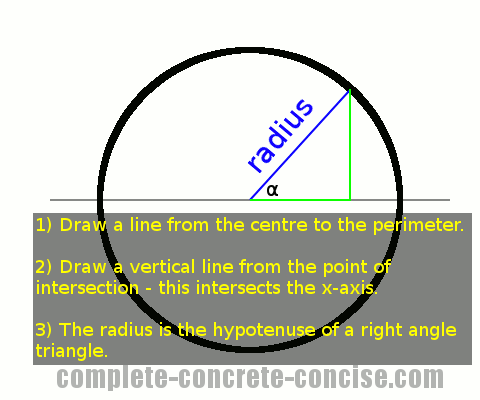
3) This line is one unit long and is the same as the radius of the circle
4) Drop a vertical line from where the radius intersects the perimeter. This line will be perpendicular to the x-axis (i.e. it intersects / crosses the x-axis and forms a 90° angle)
5) The vertical line, along with the x-axis form two sides of a right angle triangle (the two sides that join at 90° – traditionally called the opposite and adjacent sides of the right angle triangle)
6) The radius forms the hypotenuse of the right angle triangle with an angle α relative to the adjacent side (alpha is math-speak for “whatever angle you chose”)
It should be obvious that for angles between 0° and 90° we can go from a circle to an equivalent right angle triangle.
It is not obvious that this makes the mathematics of trigonometry easier or more useful.
Trigonometric Functions Using the Unit Circle
Looking at the triangle formed inside the unit circle, we see there is enough information to work out the trigonometric ratios:
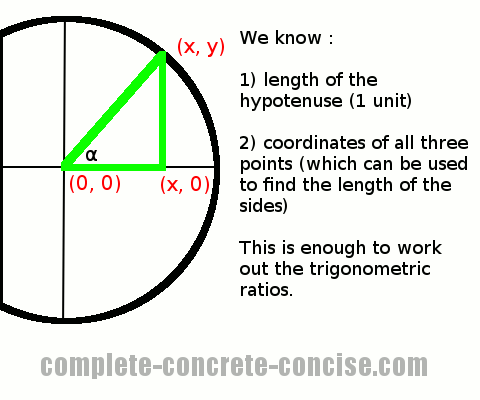
To calculate sin(α) we divide the length of the opposite side by the length of the hypotenuse.
The length of the opposite side is: |y1 – y2| (the absolute value of the difference between y-coordinates). This is either |(y – 0)| or |0 – y| (depending which way we take the difference of the coordinates), which is the same as the y-coordinate where the radius intersects the perimeter.
Lengths are always the absolute value of a difference because a triangle cannot have a side with a length less than zero. The absolute value is either explicitly stated using the absolute value operator |a – b| or implicitly done by subtracting the smaller value from the larger value.
The length of the hypotenuse is: 1 (because this is a unit circle and the hypotenuse has the same length as the radius which is exactly one unit).
Therefore, sin(α) = opposite / hypotenuse = y / 1, which is the same as y.
Note: Most math text books will define it as:
sin(α) = y / r
I think adding the r only complicates it because r = 1, so there really isn’t much point in adding it (except for strict completeness).
By using a unit circle, we can immediately find the sine of an angle by looking at the y-coordinate where the radius intersects the perimeter.
A similar derivation applies for cosine – which is the same as the x-coordinate where the radius intersects the perimeter, i.e. cos(α) = x
Note: Most math text books will define it as:
cos(α) = x / r
I think adding the r only complicates it because r = 1, so there really isn’t much point in adding it (except for strict completeness).
A similar derivation shows that tangent is y / x.
Since a unit circle is not a triangle, it is possible to measure or mark out angles greater than 90° or less than 0°.
It is reasonable to ask if this new way of finding trigonometric ratios work for angles that can never exist in a right angle triangle
Angles Greater than 90° or Less Than 0°
Consider the following radius drawn at an angle greater than 90°:

Can we use the x and y coordinates the way we did for angles between 0° and 90°?
We can draw a vertical line from where the radius intersects the unit circle and create a right angle triangle as before, but will we get the same answers?

Calculating sin(α) we see that sin(α) calculated as opposite / hypotenuse = y – just as we observed before.
Calculating cos(α) we see that cos(α) calculated as adjacent / hypotenuse ≠ x. The calculated value is positive, whereas the value of the x-coordinate is negative.
Calculating tan(α) we see that tan(α) calculated as opposite / adjacent ≠ y / x. Again, the first value is positive whereas the second value is negative.
We have the correct magnitude (numbers), but the wrong sign (positive / negative).
In the original article on trigonometric functions, I said that the tangent is the slope of the line. Clearly, the slope is negative, so using the unit circle gives us the right answer – whereas, the triangle way of calculating the tangent gives the wrong answer.
What Does All This Mean?
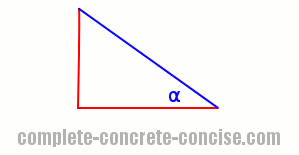
At the beginning of this article I said that angles are measured in a counterclockwise direction relative to the x-axis.
It is not possible to measure the angle α of the right angle triangle in a counterclockwise direction relative to the x-axis if the triangle is oriented this way (which is the case with the example above):
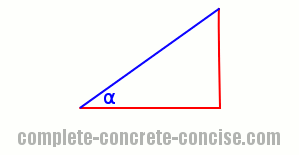
If the triangle is flipped, then it is possible to measure the angle in a counterclockwise direction:
The two triangles are mirror images of one another. The one on the left is what results with the angle is between 90° and 180° on a unit circle. The one on the right is a mirror image and occurs when we multiply the x-coordinates of the left triangle by -1:
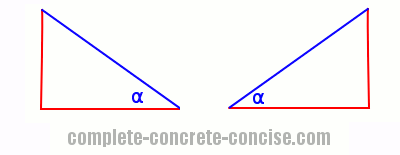
NOTE: rotating or flipping triangles does not change their properties.
NOTE: In mathematics and physics (and other sciences) when you get the wrong answer because the signs are different (positive / negative) but the magnitude (numbers) are the same, it is probably because some initial assumption was wrong.
For example, if you calculate the speed at which an asteroid is moving away from the Earth and you get an answer of -400m/s, then you know that your initial assumption (the asteroid is moving away from the Earth) is wrong – the asteroid is, in fact, moving towards the Earth.
When using the traditional (triangle) way of calculating trigonometric relations we (implicitly) orient the triangle so it is like this:

When we get a negative value, it tells us that the triangle is oriented in a different way.
Summary
- The unit circle allows us to define trigonometric values for all angles – not just those between 0° and 90°
- Using the unit circle allows us to correctly determine the slope (tangent) of a line
- Sine and cosine can be read directly off the unit circle
| Function | How to Compute | Comment |
| Sine | y | y-coordinate where the radius intersects the perimeter of the circle |
| Cosine | x | x-coordinate where the radius intersects the perimeter of the circle |
| Tangent | y / x | ratio of the y-coordinate to the x-coordinate where the radius intersects the perimeter of the circle. This is the same as the slope of the line. |
| Cosecant | 1 / y | inverse of the y-coordinate where the radius intersects the perimeter of the circle |
| Secant | 1/ x | inverse of the x-coordinate where the radius intersects the perimeter of the circle |
| Cotangent | x / y | ratio of the x-coordinate to the y-coordinate where the radius intersects the perimeter of the circle |